In the event of a frontal collision, a large amount of kinetic energy is generated.

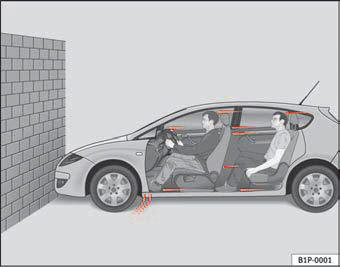
Fig. 6 Passengers of a vehicle heading for a brick wall. They are not wearing seat belts.

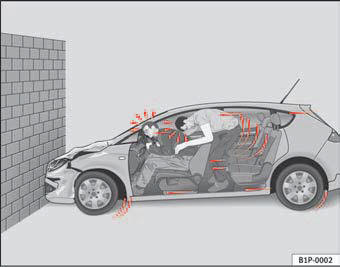
Fig. 7 The vehicle with unbelted occupants strikes the wall.

The action of the laws of physics in the case of a frontal collision may be explained in the following way: As the vehicle moves 􀂟 fig. 6 the vehicle and the passengers alike accumulate a stored energy called “kinetic energy”.

The amount of “kinetic energy” depends on the speed of the vehicle and the weight of the vehicle and passengers. The higher the speed and the greater the weight, the more energy there is to be “released” in an accident.

The most significant factor, however, is the speed of the vehicle. If the speed doubles from 25 km/h to 50 km/h, for example, the kinetic energy increases by a factor of four.

Because the passengers in our example are not restrained by seat belts, the entire amount of kinetic energy has to be absorbed at the point of impact  fig. 7.

Even at speeds of 30 km/h to 50 km/h, the forces acting on bodies in a collision can easily exceed one tonne (1,000 kg). At greater speed these forces are even higher.

Passengers not wearing seat belts are not “attached” to the vehicle. In a frontal collision they will continue to move forward at the speed their vehiThe action of the laws of physics in the case of a frontal collision may be explained in the following way: As the vehicle moves 􀂟 fig. 6 the vehicle and the passengers alike accumulate a stored energy called “kinetic energy”.

The amount of “kinetic energy” depends on the speed of the vehicle and the weight of the vehicle and passengers. The higher the speed and the greater the weight, the more energy there is to be “released” in an accident.

The most significant factor, however, is the speed of the vehicle. If the speed doubles from 25 km/h to 50 km/h, for example, the kinetic energy increases by a factor of four.

Because the passengers in our example are not restrained by seat belts, the entire amount of kinetic energy has to be absorbed at the point of impact  fig. 7.

Even at speeds of 30 km/h to 50 km/h, the forces acting on bodies in a collision can easily exceed one tonne (1,000 kg). At greater speed these forces are even higher.

Passengers not wearing seat belts are not “attached” to the vehicle. In a frontal collision they will continue to move forward at the speed their vehicle was travelling just before the impact. This example applies not only to frontal accidents, but also to all accidents and collisions.